Del círculo de quintas al círculo de Coltrane: El Dios de los números y la música.

John Coltrane, además de un gran safoxonista, fue una de las figuras más importantes de la vanguardia del jazz. Su concepción de la música fue clave en la evolución de la interpretación de este género, debido a su manera de ampliar los solos.

Coltrane, más conocido como Trane, se centró en la relación de la música y las matemáticas, ya estudiada ampliamente desde la Grecia Clásica. Precisamente por algunas de sus teorías es venerado y considerado un Dios por la African Orthodox Church.

La aplicación de sus propias teorías musicales, supuso un paso adelante en el mundo de la música, aportando un nuevo punto de vista desconocido hasta el momento.

Dios, música y matemáticas.

La vida de Coltrane fue muy ajetreada, pasó por muchas etapas que van desde problemas con las drogas hasta una fe que ponía por encima de todo, como si fuese el mayor creyente del planeta. Y fue esta ardiente fe la que le hizo superar su adicción.

El 9 de diciembre de 1964, Coltrane grabó su álbum A Love Supreme. Al principio, Coltrane quería que se llamase Allah Supreme, pero no lo hizo por miedo a represalias religiosas y políticas. Este disco fue concebido como una obra a la divinidad y en él, Coltrane se basa en un poema dedicado a Dios. Para realizarlo, cada nota está vinculada a una sílaba del poema.

En este período de sanación y salvación se volcó en la espiritualidad de la música y defendía que los sonidos tenían significados emocionales. Según esta creencia, con determinados sonidos se puede afectar a la naturaleza o incluso curar a las personas. Algo que no es del todo una locura, ya que hay determinadas ramas músico-psicológicas que atienden a estas teorías. aunque sin llevarlas tan al extremo, como la musicoterapia.

Para saber qué sonidos eran exactamente los que manipulaban las emociones o influían en la naturaleza o los animales, Coltrane creía que tenía que estudiar el origen y la composición del sonido con mucha profundidad. Esto lo llevó a investigar la relación entre las matemáticas y la música. Él creía firmemente en que cuanto más profundizase y entendiese la conexión entre las matemáticas y la música, más se acercaría al entendimiento de lo divino.

De las teorías de Einstein al Círculo de Coltrane.

Entre los estudios de Coltrane, se aprecia especialmente la influencia de las teorías de Albert Einstein. Figuras como la del físico y saxofonista Stephen Alexander argumentan las similitudes existentes entre la obra musical de Coltrane con la científica de Einstein. Sobre todo en aquello relacionado con el llamado «Círculo de Coltrane», la herramienta que había diseñado para poder modificar y extender sus solos y ofrecer una visión diferente de la música.

Se conserva un dibujo de este círculo, hecho por el mismísimo Coltrane, con anotaciones que facilitan su comprensión. Él mismo se lo entregó al saxofonista Yusef Lateef en 1967, cuando trató de explicarle su teoría entre las pausas de un concierto en el que ambos tocaban.

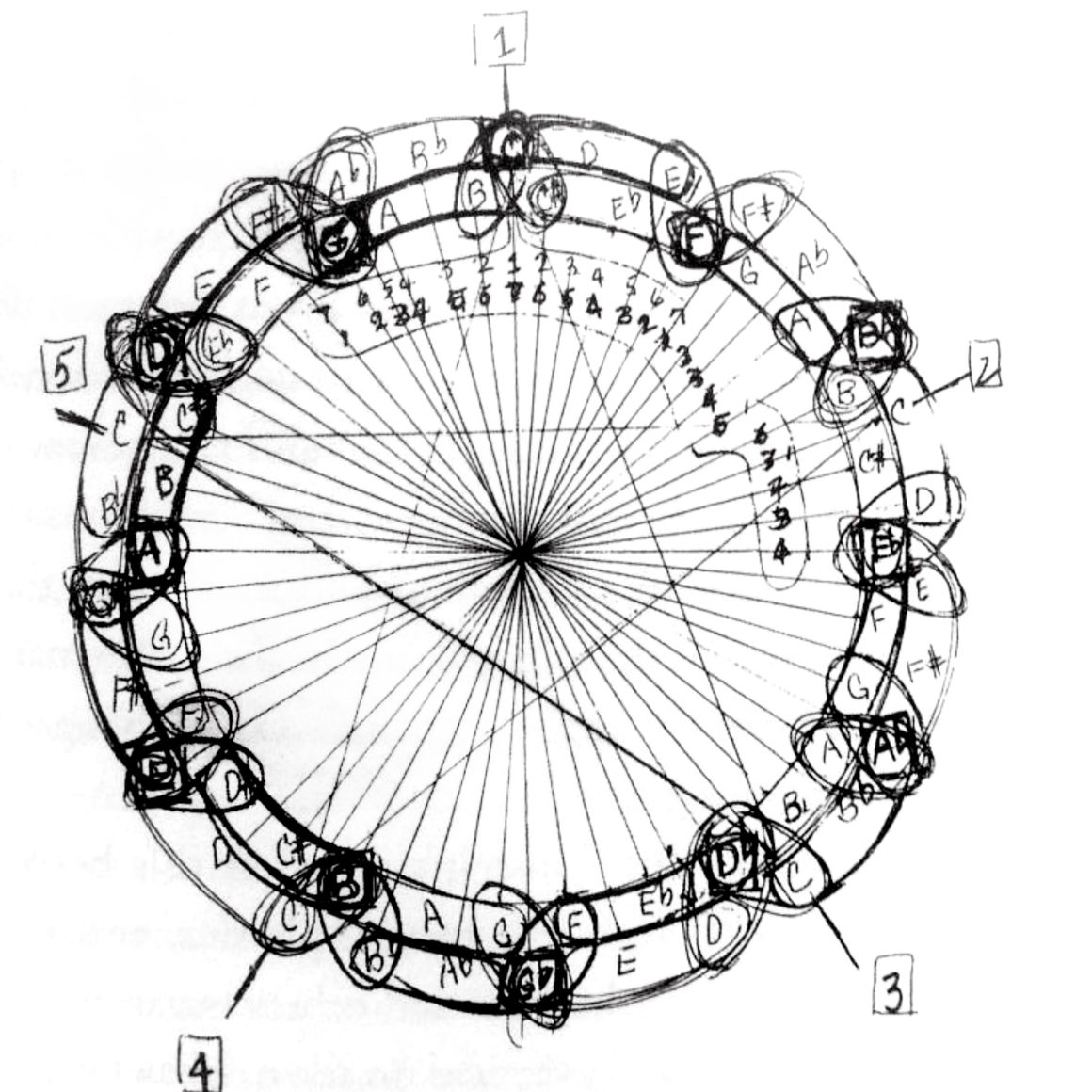
Como cabe de esperar, no todos los músicos contemporáneos a Coltrane comprendieron su teoría. Incluso hoy en día se considera complicado improvisar siguiendo su círculo, por mucho que se base en el famoso Círculo de Quintas , que ya hemos explicado en un artículo anterior. Tanto es así, que una de las piezas más temidas de la historia del Jazz es Giant Steps que, cómo no, está hecha siguiendo el Círculo de Coltrane. Es el ejemplo más importante y evidente de las teorías coltranianas.

Giant Steps.

En Giant Steps, Coltrane utilizó unas progresiones armónicas únicas que, posteriormente, aplicó a temas estandarizados del jazz. Por supuesto, los cambios de acordes de esta secuencia seguían las normas del Círculo de Coltrane, y pasaron a conocerse como los «Cambios de Coltrane» o «Progresiones/Secuencias de Coltrane«. Como decíamos antes, estos cambios no seguían las directrices a las que estaban acostumbrados los músicos del momento. Esto se hace especialmente notorio cuando escuchamos la grabación original. El momento clave llega cuando Tommy Flanagan, el pianista que toca en el disco, comienza su solo. Poco a poco la sensación que se estaba transmitiendo inicialmente al oyente se va transformando en una especie de ansiedad por lograr continuar y mantener todos esos cambios armónicos y tonales a tempo. El momento fulminante es justo cuando Coltrane comienza a tocar exageradamente rápido. Exactamente en ese momento, Flanagan se rinde y se ve obligado a dejar de tocar de golpe. Y no es que fuese un mal pianista ni mucho menos. Grandes músicos, incluso a día de hoy, opinan que se podría tocar a modo de acompañamiento siguiendo la estructura armónica, pero que intentar improvisar sobre ella es una auténtica locura, casi imposible de completar.

Para entender ese solo de piano y, en general, todo lo que sucede en Giant Step, se necesita partir de un dominio perfecto del Círculo de Quintas y su vinculación a los sonidos armónicos y los parciales.
Cuando tocamos una nota del piano, por ejemplo el do, se escuchan varias frecuencias simultáneamente. La primera de ellas, la más grande es un do, pero la siguiente importante es un sol. Por eso, la quinta (do-sol es un intervalo de quinta justa) es el intervalo más fuerte e importante musicalmente hablando. Y esta es la causa por la que el Círculo de Quintas se compone de precisamente de quintas, y también por la que muchas progresiones armónicas en muchos y diferentes estilos musicales comienzan por I-V o concluyen con V-I (la predilecta de la música clásica). En el jazz, la progresión fundamental es II-V-I.

Si deseas profundizar más en tus conocimientos sobre armónicos, te recomendamos que veas este vídeo creado por Hugo Landolfi, un experto en la materia y uno de los mejores afinadores de pianos del mundo.

Como decíamos, el círculo de Coltrane se basa en el de quintas, por lo que las progresiones de Coltrane en esta canción están llenas de giros V-I. Pero cualquier pianista estaría acostumbrado a ellas y este no sería motivo para parar de tocar. El problema se encuentra en que estos cambios V-I no se hacen en una única tonalidad, sino en 3 e incluso superpuestas. Estas superposiciones ya no son algo propio del Círculo de Quintas. Aquí ya entramos en el terreno propio de Coltrane. Él realiza uniones/desplazamientos en forma de triángulos (Mi b – Sol – Si) siguiendo terceras mayores y dividiendo así a la octava en tres partes iguales.

Para entenderlo de forma un poco más fácil, es mezclar círculos con triángulos a la hora de moverse por el círculo y así estaríamos conectando el Círculo de Quintas con el de Contrane. Haciéndolo así a lo largo de la canción, estarías tocando en las doce tonalidades. Recomendamos que veas el vídeo The most fearest song in Jazz, de VOX Earworm, si quieres profundizar más. En este vídeo, comparan este hecho con el de hablar rapidísimo árabe, español y chino en la misma conversación.

Desmenuzando el círculo.

Roel Hollander es uno de los que más ha estudiado las teorías de Coltrane y tiene publicadas dos obras al respecto: Music & Geometry y Tone Circle. Gracias a ellas sabemos que el Círculo de Coltrane es como tener dos círculos de quintas en uno, o más bien, uno dentro del otro.

De ellos, el círculo exterior es la escala de tonos enteros de Do, mientras que el interior representa la escala de tonos enteros de Si. De esta manera, podríamos desplazarnos por uno, por otro, o incluso zigzaguear entre ambos.

Es precisamente al zigzaguear cuando se nos presentan varias opciones. La primera es que si lo hacemos en sentido de las agujas del reloj, obtenemos un círculo de cuartas. Pero si zigzagueamos en sentido contrario al de las agujas del reloj, entonces tenemos un círculo de quintas.

Pero la teoría de Coltrane no termina ahí, ya que como vemos, en ambos círculos hay espacios grandes y otros subdivididos en espacios más pequeños. Es en los espacios pequeños donde quedan 4 tonos que, al combinarlos con la nota del espacio grande, nos da 6 veces la misma escala hexátona en cada cambio de tono. Para complicarlo más, las escalas hexátonas formadas en los espacios pequeños, avanzan en sentido contrario a como lo hacen las escalas hexátonas de los espacios grandes de los círculos. Así, estas nuevas escalas de tonos enteros hacen que se pueda tener la misma escala al ir ascendente (sentido de las agujas del reloj) o descendentemente (sentido contrario). Si hacemos todas estas combinaciones, de cada nota puede salir una nueva escala diferente hasta que al final, tal y como se decía en el documental, se termina improvisando o tocando en las 12 tonalidades.

Uniendo teoría y creencias aparecen pentagramas.

Como sabemos, Coltrane pretendía demostrar que matemáticas y música estan vinculadas, pero también creía que todo tenía un trasfondo que lo llevaría a entender y acercarse a lo divino. Lo que quizás no sabías es que Coltrane también era supersticioso y creía en el ocultismo. Esto también tiene su huella en su teoría musical.

Su Círculo se basa en escalas hexátonas/hexatonales. Eso ya lo hemos visto. Ahora dibujemos como él lo hacía.

¿Recuerdas que el dibujo de Coltrane parece que tiene un pentagrama invertido dibujado en su interior? Bien, no es que lo parezca, es que lo tiene. Es el resultado de hacer relaciones por terceras en los círculos y esos pasos que comentamos al hablar de la dominante y los movimientos triangulares.

A partir de ahí, si se unen los tonos de la escala del círculo de fuera, aparece un hexagrama. Además, si continuamos y también unimos o combinamos el hexagrama con el pentagrama que ya salía al inicio (recuerda el dibujo de Coltrane), obtenemos lo que se conoce como Símbolo del Doble Poder. Este símbolo representa la unión entre el microcosmos (mundo interior) y el macrocosmos que es el mundo exterior Este tema interesó a grandes compositores clásicos, como Bartók y Crumb, que compusieron obras con estos nombres (Bartók compuso el Microcosmos y Crumb el Macrocosmos).

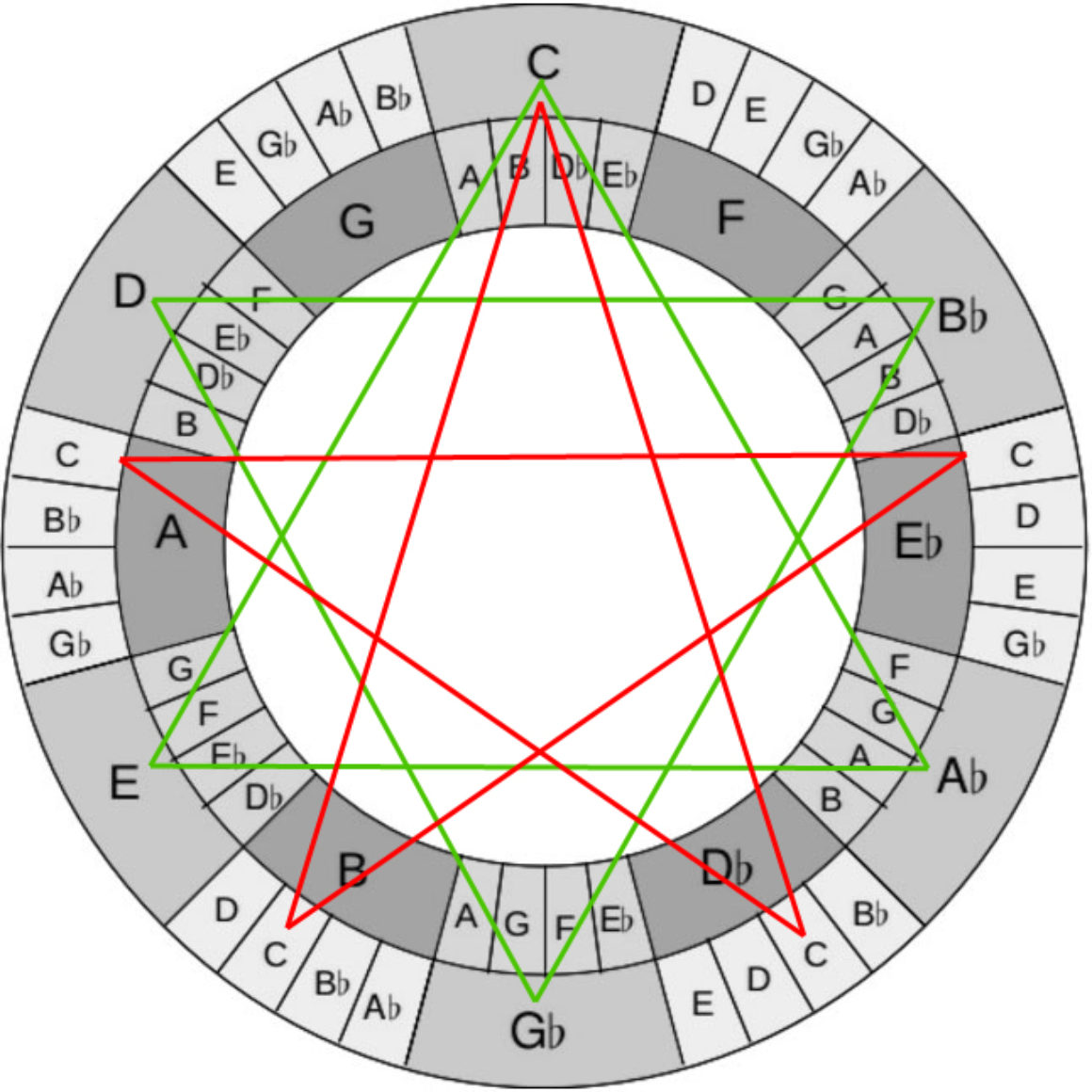
Pero el místico de Coltrane dio un paso más. No contento con pentagramas invertidos, hexagramas, la simbología del seis y el Símbolo del Doble Poder; aún quiso proseguir y llegar al Merkaba. Merkaba es como se conoce en algunas culturas al símbolo del tetracordo de la Estrella y simboliza a un espíritu ligero o un vehículo de luz divina. Pero este símbolo también representa la ley más importante de la física: la relación entre lo positivo y lo negativo (los polos).

Los números del círculo.

Sí, ya sabemos que hablamos de los símbolos, los espacios y las rayitas, pero también te has fijado en que hay números.

Los números de afuera, que son de un tamaño mayor, indican las 5 octavas que completan el círculo. Si queremos volver al simbolismo, recordar que si multiplicamos 5 octavas por 12 tonos, tenemos 60 tonos. Esto puede llevar a dos teorías: la primera es la insistencia en la simbología del 6 y la otra es la que le sirvió a algunos para rebautizar el círculo como «El reloj», porque entran 60 segundos en un minuto, 60 minutos en una hora. Todo esto se relaciona con las escalas hexátonas o hexatonales.

Dentro del círculo también hay dos filas de números, que en realidad son la misma pero invirtiendo el orden: 7-6-5-4-3-2-1-2-3-4-5-6-7 y 1-2-3-4-5-6-7-6-5-4-3-2-1. Técnicamente, los estudiosos opinan que esto es la relación cromática (o de semitonos) que hay entre los tonos enumerados en el anillo de fuera y el de dentro cuando se combinan.

Además, el 1 y el 7 son un tritono que se corresponde con DO y FA#. Como vemos, entre las rayas del 1 y del 7, hay 6 espacios entre las líneas de Coltrane (otra vez el seis que tanto le gustaba). Pero es que genio o no, esto del tritono (1-7) está relacionado con el habito jazzístico de la Sustitución del Tritono.

Si no sabes en qué consiste la sustitución del tritono, trataré de explicártelo con que me entiendas. Sin llenarte de tecnicismos ni pasos agigantados:

C7 puede ser sustituido por F#7 porque ambos tienen el tritono formado por las mismas notas. Es decir, ambos acordes presentan notas comunes en las notas que crean el tritono, que son MI y la enarmonía de SIb o LA#.

En clásico esto se suele ver más de otra manera. Cuando cadenciamos, la V7 suele resolver en la I. Pues esa V muchas veces puede sustituirse por otro acorde siempre y cuando sea de la misma especie (sea un acorde de séptima de dominante). Pero esta sustitución para poder llevarse a cabo, necesita de otro requisito: que la fundamental del nuevo acorde esté a distancia de tritono del original.

En música clásica estos acordes son tratados como acordes de sexta aumentada y surgen del movimiento cromático de las voces contrapuntísticas y por eso su resolución habitual es sobre el acorde de dominante (V).

Frecuentemente es lo que se veía como un II con la quinta rebajada, una derivación de las dominantes secundarias (V-V). Si a esto le añadimos la novena menor, tendríamos la variante de la Sexta Alemana, y si le añadimos la fundamental, entonces obtenemos la Sexta Francesa. Por eso a muchos estudiantes de clásico le choca estudiar un segundo con las sextas.

En Jazz esta teoría se asocia a los acordes alterados, que son aquellos de séptima de dominante modificados cromáticamente, y las escalas alteradas, que están hechas sobre el VII grado de la escala menor melódica.

La progresión de Giant Steps.

Si consideramos todas estas uniones y relaciones podemos considerar la opción de crear acordes en vez de notas simples. Justo así es como se obtienen las progresiones que conforman la pieza más difícil del Jazz: Giant Steps.

Los acordes que forman el hexagrama son los de los grados II y V, los más importantes en las progresiones de Jazz. Pero, a mayores, Coltrane también emplea acordes de séptima menor y séptima mayor (terceras mayores). Fruto de ellos, tendremos las escalas disminuidas que abundan en sus solos, así como las relaciones de los acordes alterados.

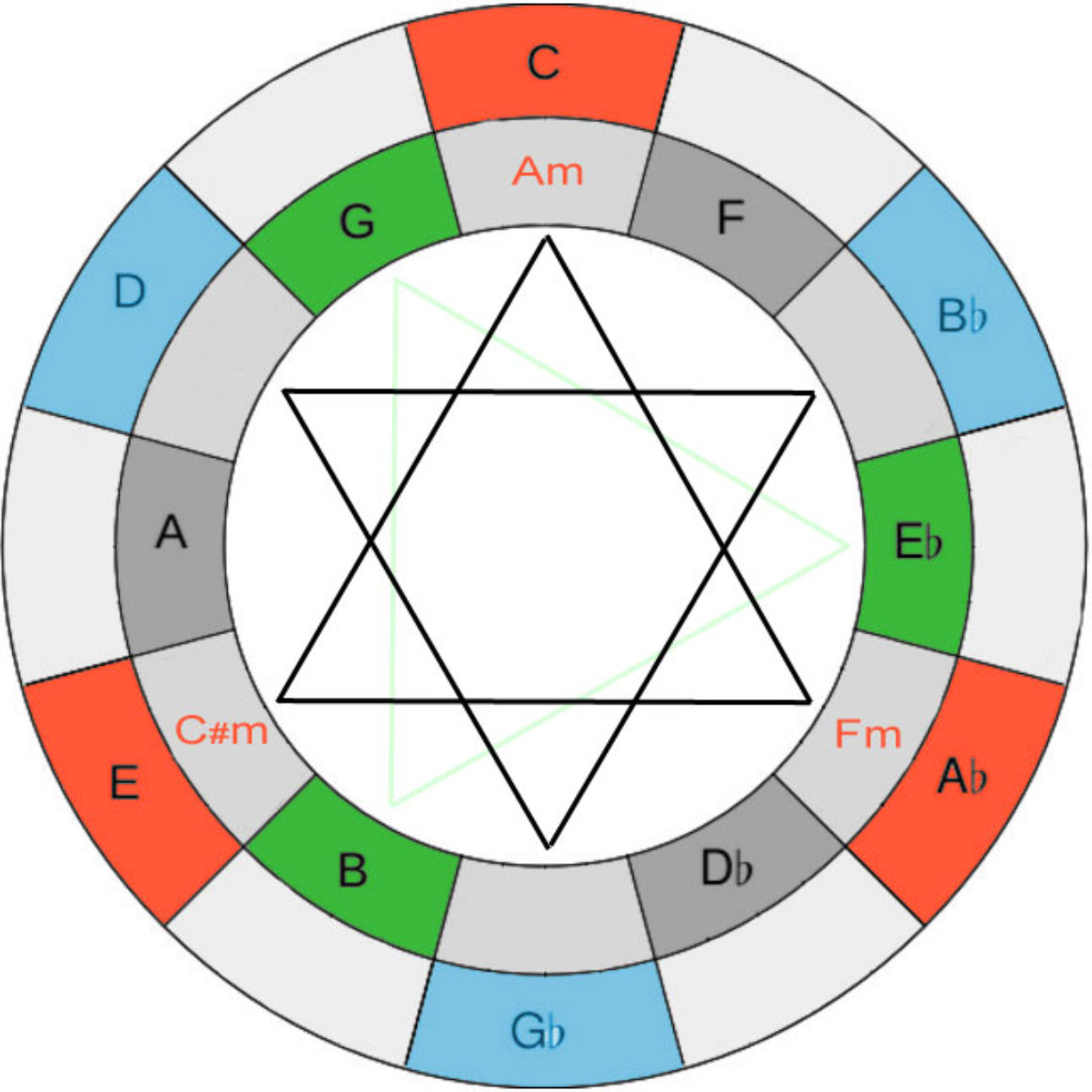
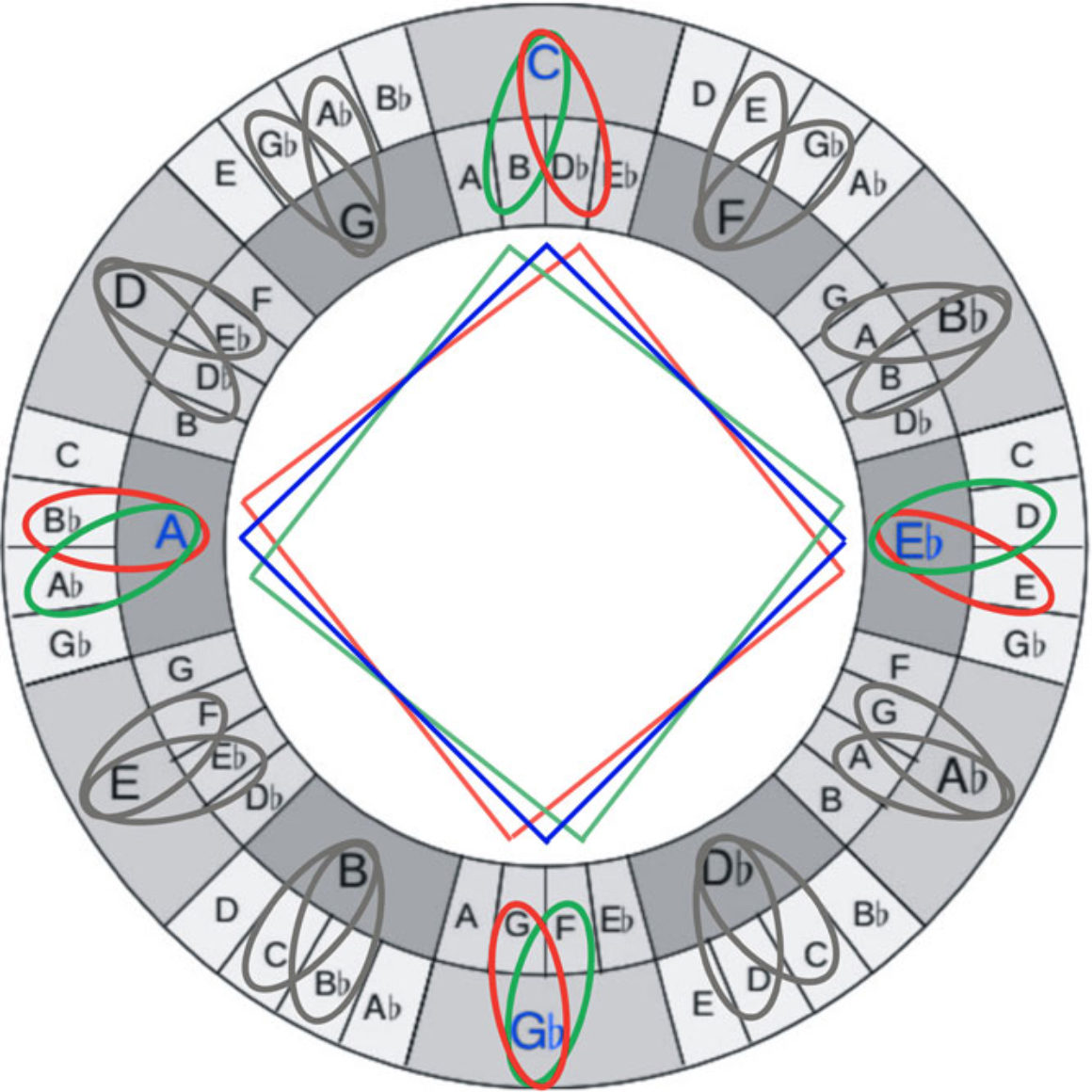
Como puedes comprobar, la figura de Coltrane supuso un cambio radical frente a la música que se venía haciendo hasta el momento. Sin embargo, lejos de ser un músico extravagante que improvisaba sin ton ni son, tras la música de Coltrane se encuentra un complejo sistema al que solo se pudo llegar tras un estudio y un entendimiento profundo de la música.